机构名称:
¥ 1.0
我们考虑在蜂窝网格(“ XYZ 2”代码)上的拓扑稳定器代码。该代码的灵感来自Kitaev Hon-Eycomb模型,是对Wootton [1]讨论的“匹配代码”的简单实现,并具有特定的边界实现。它利用了重量 - 六个(XY ZXY Z)Plaquette稳定器和重量二(XX)链接稳定器上的链接稳定器在pla-Nar六角形网格上,由2 d 2 QUBITS组成,由2 d 2 QUBITS组成,用于代码距离D,具有重量的三个固定器,在边界处稳定了一个逻辑量子。假设完美的稳定剂测量方法,我们使用最大似然解码来研究代码的性质。对于纯x,y或z噪声,我们可以通过分析求解逻辑故障率,阈值为50%。与旋转的表面代码和XZZX代码相比,这些代码仅对纯Y噪声,d 2 2 2,此处的代码距离为纯Z和纯Y噪声的2 d 2。具有有限Z偏置的噪声的阈值与XZZX代码相似,但较低的亚阈值逻辑故障率显着较低。该代码具有沿三角晶格的三个方向,具有分离的plaquette缺陷对隔离错误的分离综合征的特性,这可能对基于有效的匹配或其他近似分解的解码有用。
xyz $^2 $六边形稳定器代码
主要关键词




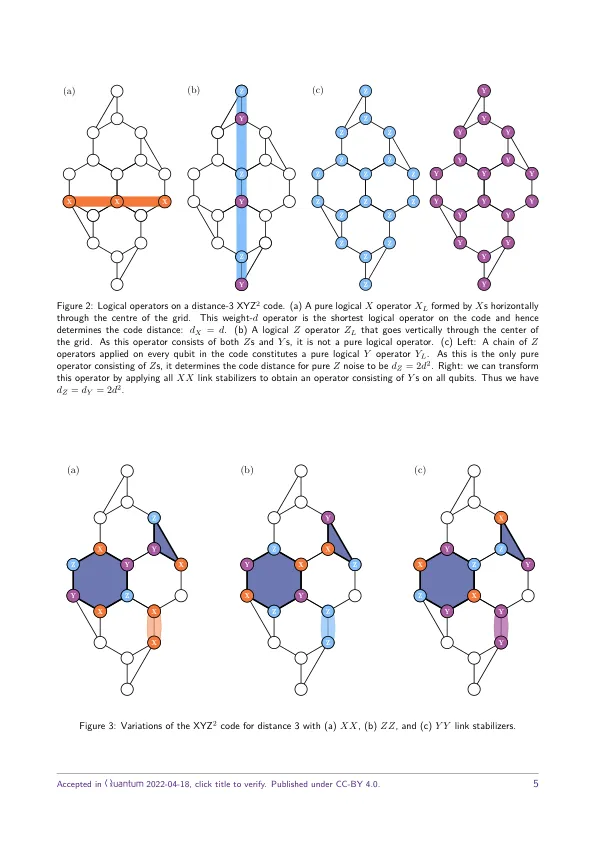

























![[[7,1,3]]代码-DTIC](/simg/8/8dc66b08f0cf1332accb96d4d418738d933225db.webp)





